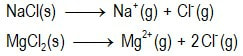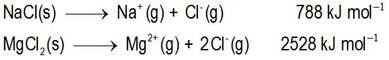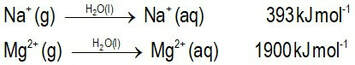|
Module 0906
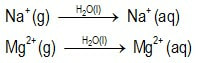
Can we predict the solubilities of ionic salts?Can we predict who will win the dissolution tug-o-war competition?
|
- HOME
-
LEARNING MODULES
- Chapter 02 Stuff, matter: What is it? >
-
Chapter 05 Chemical reactions and chemical equations
>
- 0500 Chemical reactions and chemical equations. Overview
- 0501 Chemical amount and its unit of measurement, mole
- 0502 The Avogadro constant: How many is that?
- 0503 The Avogadro constant: Why is it that number?
- 0504 Chemical formulas: What can they tell us??
- 0505 Chemical equations: What can they tell us?
- 0506 Limiting reactants: How much reaction can happen?
- 0507 Balanced chemical equations: What are they?
- 0508 Chemical reactions as competitions
-
Chapter 09 Aqueous solutions
>
- 0901 What is a solution? And what is not?
- 0902 Miscibility of liquids in each other
- 0903 Like dissolves like? Shades of grey
- 0905 Dissolution of ionic salts in water: A competition
- 0906 Can we predict solubilities of salts?
- 0907 Solution concentration
- 0908 Chemical species, speciation in aqueous solution
- 0909 Solutes: Electrolytes or non-electrolytes?
- 0910 Electrolytes - strong or weak?
- 0911 Concentrated, dilute, strong, weak
- 0912 Species concentration vs. solution concentration
- 0913 Weak electrolytes: Getting quantitative
- Chapter 11: Dynamic chemical equilibrium >
- Chapter 22 Evidence from spectroscopy >
-
ENVIRONMENTAL CHEMISTRY
>
-
EARTH'S ATMOSPHERE
>
-
Chapter 27 The greenhouse effect, climate change
>
- 2700 The greenhouse effect: overview
- 2701 Is Earth in energy balance?
- 2702 CO2 in the atmosphere before 1800
- 2703 So little CO2! Pffft?
- 2704 Does CO2 affect Earth's energy balance?
- 2705 The "greenhouse effect"
- 2706 Why does CO2 absorb radiation from Earth?
- 2707 The "enhanced greenhouse effect"
- 2708 Why doesn't CO2 absorb the radiation from the sun?
- 2709 Why are N2 and O2 not greenhouse gases?
- 2710 Doesn't water vapour absorb all the IR?
- 2711 Carbon dioxide from our cars
- 2712 The source of energy from combustion
- 2713 Comparing fuels as energy sources
- 2714 Methane: How does it compare as a GHG?
- 2715 Different sorts of pollution of the atmosphere
- 2716 "Acidification" of seawater
-
Chapter 27 The greenhouse effect, climate change
>
- FUELS
- EARTH'S OCEANS AND WATERWAYS
-
EARTH'S ATMOSPHERE
>
-
TEACHERS' CORNER
- NAVIGATION