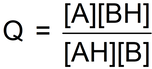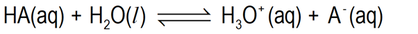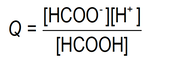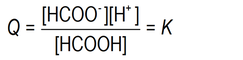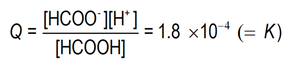Module 0913
Weak electrolytes: Getting quantitative
The law of equilibrium: using mathematics
All Qs lead to K
Can we calculate the percentage of a weak electrolyte that is ionised at equilibrium?
Different weak electrolytes, different K. So?
Prior knowledge assumed
Before delving into this module, you should have some familiarity with the following:
If a solute is a weak electrolyte, in aqueous solutions only some of the solute molecules are ionised. See Module 0910 Electrolytes – strong or weak?
This is because the ionisation reaction has reached a condition of dynamic chemical equilibrium – when the opposite reactions are proceeding at the same rate: the rate of ionisation of solute molecules is the same as the rate of association of the ions. See Module 1101 Visualising dynamic chemical equilibrium.
Before delving into this module, you should have some familiarity with the following:
If a solute is a weak electrolyte, in aqueous solutions only some of the solute molecules are ionised. See Module 0910 Electrolytes – strong or weak?
This is because the ionisation reaction has reached a condition of dynamic chemical equilibrium – when the opposite reactions are proceeding at the same rate: the rate of ionisation of solute molecules is the same as the rate of association of the ions. See Module 1101 Visualising dynamic chemical equilibrium.
Prof Bob's video not available for now. It is in Cannes, awaiting judgement on best foreign film of the year.
KEY IDEAS - Weak electrolytes: getting quantitative
The law of equilibrium
In this module, the law of equilibrium is discussed particularly in relation to solutions of weak electrolytes. A more general discussion applicable to all systems at equilibrium (including solutions of weak electrolytes) is presented in Module 1103 Equilibrium constants: The law of equilibrium.
Let’s use a generalised chemical equation for any reaction in which the reaction mixture involving the species A, B, C, and D has come to the state of dynamic chemical equilibrium:
Remarkably, we can define an expression (symbol Q, called the reaction quotient) in the following way:
Why is this expression remarkable? Well first, but not so remarkable …
In a particular reaction mixture (such as an aqueous solution) in the condition of chemical equilibrium, the concentrations of all reactant and products no longer change, the numerical value of Q does not change – it comes to a constant value because the opposite reactions happen simultaneously at the same rate. Well of course it does, because the concentrations of each species is no longer changing.
In a particular reaction mixture (such as an aqueous solution) in the condition of chemical equilibrium, the concentrations of all reactant and products no longer change, the numerical value of Q does not change – it comes to a constant value because the opposite reactions happen simultaneously at the same rate. Well of course it does, because the concentrations of each species is no longer changing.
But more, more, more remarkably ……
Trumpets and drums! Prepare to be amazed and excited!
In all reaction mixtures containing these species at equilibrium, no matter how they were made up, the numerical value of Q is the same in all of them – if all of the solutions are at the same temperature.
The symbol that is used to represent the numerical value of Q in the particular condition that the reaction is at equilibrium is K – called the equilibrium constant
So, for any reaction in a condition of dynamic equilibrium, we can write:
Trumpets and drums! Prepare to be amazed and excited!
In all reaction mixtures containing these species at equilibrium, no matter how they were made up, the numerical value of Q is the same in all of them – if all of the solutions are at the same temperature.
The symbol that is used to represent the numerical value of Q in the particular condition that the reaction is at equilibrium is K – called the equilibrium constant
So, for any reaction in a condition of dynamic equilibrium, we can write:
The law of equilibrium is perhaps the most important relationship that you will encounter in chemistry. So ….
Repeat, repeat, repeat …..
In all reaction mixtures at the same temperature in which a particular chemical reaction is at chemical equilibrium, no matter how they are made up, we can define an expression (symbol Q) that has the same value (K) in all of the mixtures.
As the concentrations of reaction species changes during reaction, the value of the expression Q changes until the reaction comes to dynamic chemical equilibrium. In all reaction mixtures at the same temperature, Q comes to the same value. We call that particular value the equilibrium constant (symbol K).
This is despite the fact that the concentrations of the various reaction species may be different from reaction mixture to reaction mixture.
For each reaction, the numerical value K changes with temperature.
At any given temperature, the numerical value K is different from reaction to reaction.
Repeat, repeat, repeat …..
In all reaction mixtures at the same temperature in which a particular chemical reaction is at chemical equilibrium, no matter how they are made up, we can define an expression (symbol Q) that has the same value (K) in all of the mixtures.
As the concentrations of reaction species changes during reaction, the value of the expression Q changes until the reaction comes to dynamic chemical equilibrium. In all reaction mixtures at the same temperature, Q comes to the same value. We call that particular value the equilibrium constant (symbol K).
This is despite the fact that the concentrations of the various reaction species may be different from reaction mixture to reaction mixture.
For each reaction, the numerical value K changes with temperature.
At any given temperature, the numerical value K is different from reaction to reaction.
Applying the law of equilibrium to a particular case: methanoic acid
An aside .... just explaining
Using a generalised equation for ionisation of a weak electrolyte solute which is an acid, the equilibrium reaction can be represented as follows:
Or, to better show the involvement of water molecules in breaking the H-A bonds:
We will use the first – just because it is simpler, even if not such an accurate description.
End of aside. And now back to the story .....
Let’s zoom in to talk about aqueous solutions of a particular solute which is a weak electrolyte: methanoic acid (or, formic acid), represented by the chemical equation
End of aside. And now back to the story .....
Let’s zoom in to talk about aqueous solutions of a particular solute which is a weak electrolyte: methanoic acid (or, formic acid), represented by the chemical equation
We write the reaction quotient expression in the defined way:
… where the values in square brackets are the actual species concentrations (See Module 0912 Species concentration vs solution concentration).
In all solutions in which this reaction is at equilibrium, and at the same temperature, the numerical value of Q is the same. The symbol for that numerical value is K. i.e., at a given temperature ...
In all solutions in which this reaction is at equilibrium, and at the same temperature, the numerical value of Q is the same. The symbol for that numerical value is K. i.e., at a given temperature ...
And it doesn’t matter if we are considering a solution made by dissolving …
- 1.0 mol of methanoic acid in 1 L of solution, or
- 0.001 mol of methanoic acid in 1 L of solution, or
- 0.02 mol of H+(aq) ions (as HCl) and 0.75 mol of HCOO-(aq) ions (as HCOO-Na+) or
- 0.5 mol of methanoic acid and 0.01 mol of H+(aq) ions (as HCl) or
- any other amounts of these reaction species (‘reactants’ and ‘products’) to any volume.
Time for quantitative calculations
We will use experimentally determined values of K of various weak electrolytes – listed in many places.
In our case, the numerical value of Q in all aqueous methanoic acid solutions at chemical equilibrium at 20 °C is 1.8 x 10-4
So, in all solutions in which this reaction is in equilibrium at 20 °C ....
We can use this data to calculate the fraction of HCOOH that is ionised in a 0.100 M aqueous HCOOH solution, as follows. Here we go ....
And for solutions of weak electrolytes with smaller values of K …..
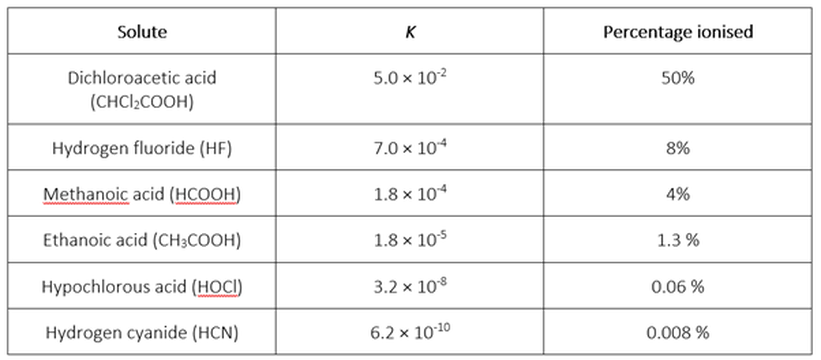
If you do this for a number of weak electrolytes in aqueous solution with c(solute) = 0.100 M at 20 °C, you will derive the percentages ionised in each case shown in the following table:
We can see that the smaller K for a weak electrolyte in aqueous solution, the lower is the percentage of solute ionised – that is, a weaker electrolyte.
Takeaway messages: Aqueous solutions of weak electrolytes
The main takeaway messages from this module, apart from how to do typical calculations are:
- The different strengths of different weak acids can be expressed quantitatively via the values of their equilibrium constants (K) – all at the same temperature.
- For a given weak electrolyte HX, no matter how a mixture is made up containing the species HX(aq), X-(aq) and H+(aq), the concentrations of the species change until the value of the reaction quotient (symbol Q) in the solution becomes equal to the value of the equilibrium constant (symbol K) appropriate for that electrolyte at the temperature of the solution. Then, the ionisation reaction is in the condition of dynamic chemical equilibrium.
So what?
Well, two very important applications of this mathematical treatment are the application of the law of equilibrium to the following situations:
Speciation: If the concentration of H+(aq) ions in a solution is changed (that is, [H+] and pH are changed), the relative amount of the species HX(aq) molecules and X-(aq) ions changes. See a not-very-detailed discussion in Module 0908 Chemical species, speciation in aqueous solution. A more quantitative presentation will be made in a module in Chapter 12 Acids and bases.
Buffer solutions: If the concentrations of HX(aq) molecules and X-(aq) ions in solution are relatively large, variation of the relative amounts of these two species can be used to control the concentration of H+(aq) ions (ie, pH) in solution. A quantitative discussion will be presented in a module in Chapter 12 Acids and bases.
Speciation: If the concentration of H+(aq) ions in a solution is changed (that is, [H+] and pH are changed), the relative amount of the species HX(aq) molecules and X-(aq) ions changes. See a not-very-detailed discussion in Module 0908 Chemical species, speciation in aqueous solution. A more quantitative presentation will be made in a module in Chapter 12 Acids and bases.
Buffer solutions: If the concentrations of HX(aq) molecules and X-(aq) ions in solution are relatively large, variation of the relative amounts of these two species can be used to control the concentration of H+(aq) ions (ie, pH) in solution. A quantitative discussion will be presented in a module in Chapter 12 Acids and bases.
SELF CHECK - Some thinking tasks
ANSWERS
Finding your way around .....
You can browse or search the Aha! Learning chemistry website in the following ways:
You can browse or search the Aha! Learning chemistry website in the following ways:
- Use the drop-down menus from the buttons at the top of each page to browse the modules chapter-by-chapter.
- Click to go to the TABLE OF CONTENTS (also from the NAVIGATION button) to see all available chapters and modules in numbered sequence.
- Click to go to the ALPHABETICAL INDEX. (also from the NAVIGATION button).
- Enter a word or phrase in the Search box at the top of each page.