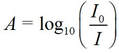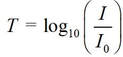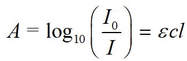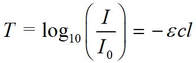Module 2204
Beer’s law: How much light is transmitted?
Solutions containing a coloured species
What fraction of light is transmitted?
What does the fraction depend on?
Concentration?
Path length?
Wavelength of light?
North of the equator, or south?
Coloured solutions of a particular solute can range from 100% transparent (all incident light is transmitted, none absorbed) to totally opaque (all incident light absorbed, none transmitted). Prof Bob clarifies the factors that govern the fraction of light transmitted. Quantitative calculations give rise to an important analytical method.
Remember that Beer's law is applicable to solutions of a particular solute, and a particular wavelength of light.
KEY IDEAS - Beer’s law: How much light is transmitted?
The same species in the two solutions, at the same concentration, and the same path length travelled by the light before reaching our eyes. Perhaps not surprising that the colour intensity is the same?
Reflect on our general experiential knowledge
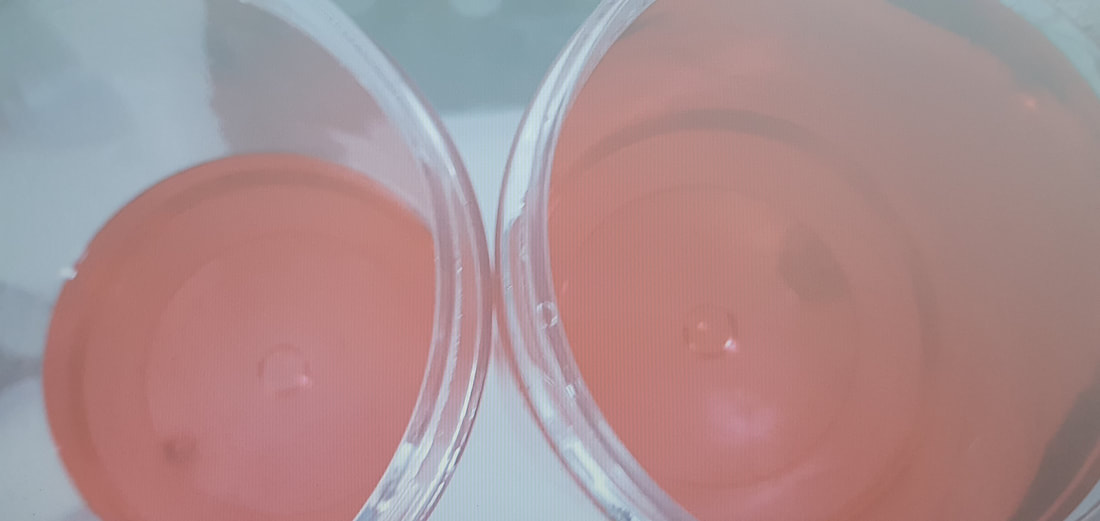
Look through a coloured solution in a colourless container. It may appear red, for example, if species (such as molecules or ions) absorb “blue wavelengths” from the white light that enters the solution from the other side. Or it may appear blue or green because of absorption of “red wavelengths” and “yellow wavelengths”.
[And the light absorption can be attributed to “excitation” of electrons in the species to higher “allowed” energy levels - as discussed in Module 2201 Quantisation of forms of energy and Module 2203 Ultraviolet-visible spectroscopy.]
What happens if we dilute a coloured aqueous solution by adding water? Of course, the colour becomes fainter. (But, if you have watched the video, you will know that this depends on where you are looking from.)
We say that the colour has become less intense, or less deep.
This does not mean that the colour changes. No, the tint remains the same. The wavelengths being transmitted (and absorbed) do not change. It is just that a smaller fraction of the incoming light (at the same wavelengths) is absorbed.
[And the light absorption can be attributed to “excitation” of electrons in the species to higher “allowed” energy levels - as discussed in Module 2201 Quantisation of forms of energy and Module 2203 Ultraviolet-visible spectroscopy.]
What happens if we dilute a coloured aqueous solution by adding water? Of course, the colour becomes fainter. (But, if you have watched the video, you will know that this depends on where you are looking from.)
We say that the colour has become less intense, or less deep.
This does not mean that the colour changes. No, the tint remains the same. The wavelengths being transmitted (and absorbed) do not change. It is just that a smaller fraction of the incoming light (at the same wavelengths) is absorbed.
Getting quantitative: Beer's law
Here is the key to sense-making of this module: The intensity of colour of a red solution depends upon how many of the blue-absorbing species’ molecules or ions interact with the incoming light before it comes to our eyes (or another sensor). The more molecules or ions that the light interacts with, the more blue light is absorbed, and the more intense is the red colour.
And the number of molecules with which passing light interacts is dependent on the concentration of the solution (symbol c), and how far the light travels through the solution before reaching our eyes (the path length, l)
Quantitatively, chemists’ use a measure of how much light of a given wavelength is absorbed by a solution called the absorbance, A, defined by
Here is the key to sense-making of this module: The intensity of colour of a red solution depends upon how many of the blue-absorbing species’ molecules or ions interact with the incoming light before it comes to our eyes (or another sensor). The more molecules or ions that the light interacts with, the more blue light is absorbed, and the more intense is the red colour.
And the number of molecules with which passing light interacts is dependent on the concentration of the solution (symbol c), and how far the light travels through the solution before reaching our eyes (the path length, l)
Quantitatively, chemists’ use a measure of how much light of a given wavelength is absorbed by a solution called the absorbance, A, defined by
where Io is the intensity of incident light (that entering the solution), and I is the intensity of transmitted light (that emerging from the solution and coming to our eyes, or a sensor).
I prefer to think in terms of a reverse measure called transmittance, T, defined as
I prefer to think in terms of a reverse measure called transmittance, T, defined as
because I can imagine more easily the fraction of incident light that is transmitted (I/Io) – rather than how many times more intense is the incident light rather compared with the transmitted light.
The extent to which the absorbance of a solution depends upon the concentration of absorbing species and the path length is given by Beer’s law (sometimes referred to as the Beer-Lambert law):
The extent to which the absorbance of a solution depends upon the concentration of absorbing species and the path length is given by Beer’s law (sometimes referred to as the Beer-Lambert law):
where the value of ε (Greek epsilon) is a characteristic of the absorbing species. (At the same concentration of solution, and through the same path length, some species absorb more intensely than others.)
Alternatively, and absolutely equivalently:
Alternatively, and absolutely equivalently:
Making sense of Beer's law intuitively
The logarithmic nature of the absorbance relationship can be visualised as follows. Suppose that 20% of light of a particular “blue wavelength” is absorbed when it passes through a 1.0 cm path length of a solution of given concentration. That is, 80% is transmitted, and I/Io = 0.20.
How much of the incident light would be absorbed if it passed through a 4 cm path length (same concentration of solution, same wavelength of incident light)? The answer is not 4 ×20%. That would lead to crazy answers if 40% were absorbed in a 1 cm pathlength. 160% absorbed over a 4 cm path length? Nonsense!
Here goes …
- Over the first 1 cm of path, 0.20 of the incident light is absorbed, and 0.80 transmitted.
- The 0.80 transmitted can be regarded as incident on the front of the second 1 cm path length section. Over the second 1 cm of path, 0.20 of 0.80 (0.16) of the (originally) incident light is absorbed, and 0.80 of 0.80 (0.64) is transmitted.
- Over the third 1 cm of path, 0.20 of 0.64 (0.128) of the (originally) incident light is absorbed, and 0.80 of 0.64 (0.512) is transmitted.
- Over the fourth 1 cm of path, 0.20 of 0.512 (0.102) of the (originally) incident light is absorbed, and 0.80 of 0.512 (0.41) is transmitted.
So, allowing for rounding off of numbers, 0.41 of the (originally) incident light is transmitted, and the fraction absorbed is 0.20 + 0.16 + 0.13 + 0.10 = 0.59. It all computes.
As well as to follow this intuitive argument, you might want to apply Beer’s law to this situation.
An application to analysis of solution concentrations
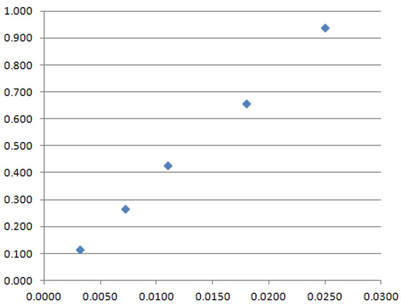
Beer's law can be used to estimate the concentration of an absorbing species in solution. First, a set of “standard” (known concentration) solutions is made up, and their absorbance over a defined path length, at a given wavelength, is measured. A plot of A vs molar concentration can be plotted as a straight line. The absorbance of the solution of unknown concentration allows its concentration to be estimated.
For example:
Solutions of a particular reagent are made up, and their absorbances measured at a defined wavelength (usually close to the maximum of its absorption peak) as it passes through a cell 5 cm long. The measurements are tabulated:
Solutions of a particular reagent are made up, and their absorbances measured at a defined wavelength (usually close to the maximum of its absorption peak) as it passes through a cell 5 cm long. The measurements are tabulated:
The solution of unknown concentration had an absorbance of 0.78, measured in the same cell and at the same wavelength. What is the concentration of the absorbing species?
The data of concentration (horizontal axis) and absorbance (vertical axis) form a straight-line plot, shown here.
You can manually draw a line of best fit, or use a graphing program to calculate the formula for the line of best fit. By either means, interpolation of a value 0.78 for the absorbance leads to a decision that the concentration of the unknown solution is 0.021 mol L-1 (2.1 x 10-2 mol L-1).
Post script: Solution UV-visible spectra
Beer’s law applies to solutions of a particular substance, and light of a particular wavelength.
For a particular coloured solute species in solution, having a particular concentration, the percentage of light transmitted (and absorbed) over a particular path length of light, is different from wavelength to wavelength.
In other words, the extinction coefficient, ε, in Beer’s law, is different at every wavelength.
And this is another way of referring to the spectrum in the visible light region of a substance (Module 2203 Ultraviolet-visible spectroscopy).
For a particular coloured solute species in solution, having a particular concentration, the percentage of light transmitted (and absorbed) over a particular path length of light, is different from wavelength to wavelength.
In other words, the extinction coefficient, ε, in Beer’s law, is different at every wavelength.
And this is another way of referring to the spectrum in the visible light region of a substance (Module 2203 Ultraviolet-visible spectroscopy).
Absorption spectrum of a copper sulfate solution. There is only low absorbance (high transmittance) of blue light. The extinction coefficient for the coloured species, Cu2+(aq) ions, is much higher at 700 nm (red light) than at 600 nm (yellow-orange).
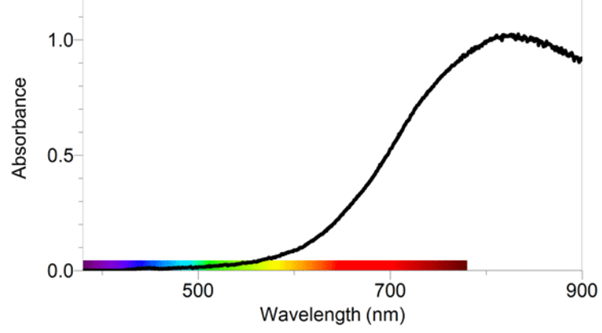
Absorbance at wavelengths less than 500 nm (blue light) is negligible, so transmittance of incident light is almost 100%. A particular solution of copper sulfate absorbs a bigger percentage of incident light with wavelength 700 nm (red light) than it does at 600 nm (yellow-orange light). Conversely, the solution transmits a bigger fraction of light at 600 nm than of light at 700 nm.
In other words, the extinction coefficient used in a Beer's law application to copper sulfate solution is larger for light of wavelength 700 nm, than at 600 nm.
So, an absorption spectrum is essentially a plot of the extinction coefficient for that solute species over a range of wavelengths.
Northern hemisphere, or southern hemisphere?
To date, there has been no reported difference.
Teachers' note: Pedagogical content knowledge
For a discussion of the activity presented in the video, go to Teachers' Corner page PCK2204 Beer's law: An activity.
For a discussion of the activity presented in the video, go to Teachers' Corner page PCK2204 Beer's law: An activity.
SELF-CHECK - Some thinking tasks
The solution on the right is made by diluting a solution identical to that on the left. The colour is much less intense. Explain.
|
But the colour intensity of the two solutions cannot be distinguished if we look from above. Explain that! Something to do with how many molecules the light interacts with along its path.
|
Finding your way around .....
You can browse or search the Aha! Learning chemistry website in the following ways:
You can browse or search the Aha! Learning chemistry website in the following ways:
- Use the drop-down menus from the buttons at the top of each page to browse the modules chapter-by-chapter.
- Click to go to the TABLE OF CONTENTS (also from the NAVIGATION button) to see all available chapters and modules in numbered sequence.
- Click to go to the ALPHABETICAL INDEX. (also from the NAVIGATION button).
- Enter a word or phrase in the Search box at the top of each page.
